Neural population-based approaches have opened new windows into neural computations and behavior

We’ve all been there. We give an impassioned spiel to a colleague on our favorite new technique, extolling its wonders and virtues. Then your colleague then looks at you, concerned, and asks the ubiquitous question: “But what have we learned about the brain?” For me, this exchange happens regularly on the topic of neural manifolds, a concept that permeates much of my research work. These neural manifolds—which reflect the assumption that geometric structure constrains the dynamics of neural population activity—are an increasingly popular lens through which to view the brain. This population-centric view provides a compact means to describe and study neural computations and the relationships between brain activity and animal behavior. Yet critics often assert that neural manifolds have yielded no new insights over classic studies of single neurons.

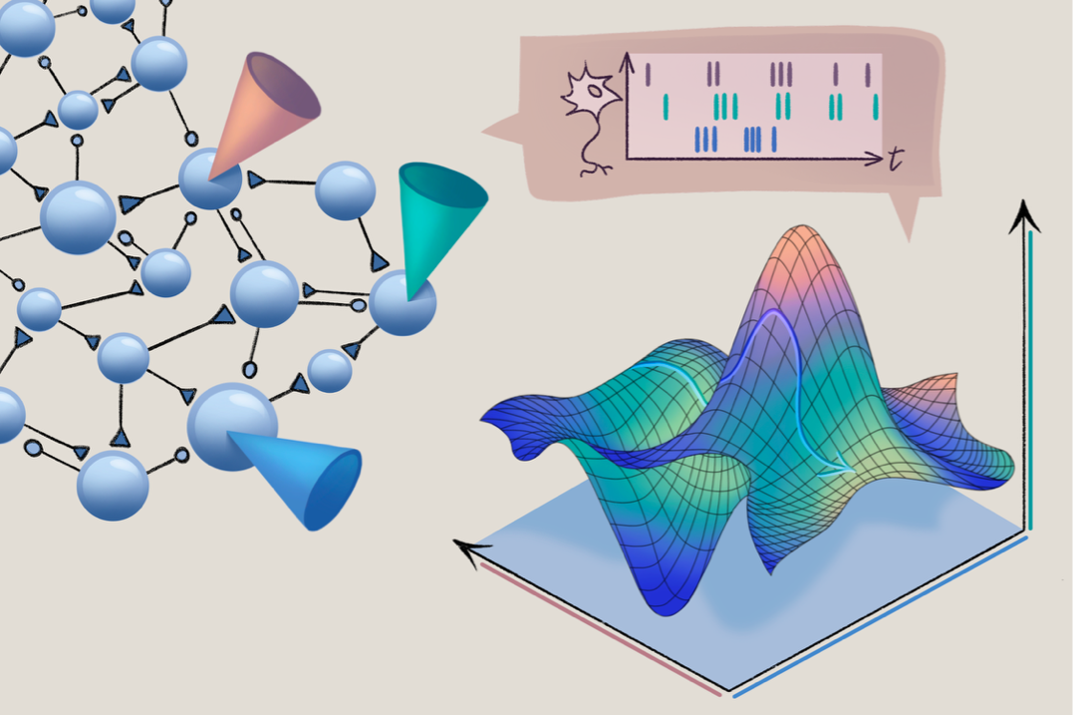
In a previous essay, I argued that neural manifolds are a conceptually appealing level to formulate theories about the brain, precisely because they capture aspects of neural computations directly at the population level. The neural manifold framework is still in its early days, but innovative new work is coming out at a rapid pace, expanding and refining how we can use manifolds to think about the brain. This includes RATS, a powerful manifold learning tool to unwrap complex geometries into digestible representations, and clever neuroscience-specific tools such as MARBLE or CEBRA, which aim to identify compact representations of behavior-specific patterns in neural population activity.

There’s still much to understand, such as the assumptions and mathematical details of neural manifolds that are most relevant for the brain’s computations (and which techniques can best uncover them). But the field of neuroscience has already greatly benefited from their use, providing foundational insights the impact of which are just now being appreciated. In this essay, I review just a few of the most exciting examples of how a manifold view has improved our understanding of the brain.

O

ne of the first successes of the neural manifolds view was to help resolve previously perplexing features of individual neural responses, which often exhibit complex and mixed representations across stimuli or behavioral contexts. In 2014, Matthew Kaufman and his colleagues used population geometry in the motor system to provide a compelling theory for a long-standing question in motor control: Given that the same motor cortical neurons are active during both premovement preparation and active movement, how do we prepare movements without executing them?

Traditional theories to explain how the arm remains still during preparation include activity thresholds or spinal gating. Kaufman and his colleagues instead demonstrated that the processes of movement preparation and movement execution can be separated within a single population by occupying different (orthogonal) dimensions within a putative neural manifold (figure below). In other words, as an animal prepares to move, neural activity traverses in one specific direction in the neural population state space. When the animal evokes the muscle contractions to cause that movement, activity spills into a separate, orthogonal set of dimensions.

Around the same time as the Kaufman paper, a study of visual decision-making offered another example of how manifold geometries can help keep different types of information—such as cue and color—distinct, even within the same neural population. Their findings have proven to be transformative (indeed, this study was recently acknowledged as a life-changing paper in a Transmitter article by Marino Pagan). Importantly, in both these studies, the geometry of these respective dimensions was crucial: The orthogonality of the dimensions (preparation versus movement or color versus cue) separated their influence on putative downstream readouts. This insight was made possible by thinking about neural manifolds and how they constrain neural population activity.

The second successful approach explores how neural manifold geometry underlies flexible behavior. Animals behave in different ways based on their surroundings and needs. Intriguingly, the same sets of neurons can be active during different behaviors, begging the question: How do the same neurons encode a rich behavioral repertoire? The Kaufman study provides an early example, and several studies published in the past 10 years have shown how a similar type of functional separation of neural processes into independent dimensions along the manifold can lead to flexible behavior. One paper demonstrated that such orthogonal dimensions enable animals to simultaneously plan and execute movements, and my own work has shown how modifying activity specifically in these planning dimensions accelerates motor learning.

Among my favorite examples of how neural manifold geometries shape behavior is a study by Hansem Sohn, Devika Narain, Nicolas Meirhaeghe and Mehrdad Jazayeri, who trained monkeys to estimate timing intervals. They identified neural manifolds in dorsal medial frontal cortex population activity, enabling them to study how the brain kept track of the learned time interval. One could imagine that the length of time could be tracked by the speed of neural trajectories on this manifold, with longer intervals corresponding to slower speeds, and downstream readout regions could monitor this speed to estimate how much time has passed. Remarkably, the authors found a more complex story under conditions where the interval is uncertain: Although speed could be used to track time, more uncertain time intervals corresponded to manifolds with greater curvature, ensuring that–for a given trajectory speed–neural trajectories were biased toward the average expected interval. The findings suggest that in contrast to the classic notion of timekeeper cells, neurons in the prefrontal cortex could track internal states of time by modifying their manifold geometry. I expect that the geometry of neural manifolds and the speed of activity along them is fundamental to our most basic behaviors.

Lastly, neural manifolds have been used to expose universal principles across individuals. Our brains reflect a fascinating trade-off between inheritance and individuality. We all share common ancestors and origins, which implies common mechanisms across all individuals of a species. Yet the computations underlying our behaviors are implemented by fully unique sets of neurons in an immensely complex biophysical regime. Resolving this paradox is one of the most exciting use cases of neural manifolds, because it makes it possible to abstract away relevant features of behavioral computations from their low-level implementations. Work from my lab and my colleagues, for example, found that different individuals performing similar behaviors had very similar structure in neural population activity.

Other labs have dug even deeper. A study on C. elegans showed that neural manifolds estimated from genetically specified cells common across different individuals have near-identical geometric organization for locomotion behaviors. In mammals, cells recorded from rodents during spatial navigation in both entorhinal cortex and the thalamus show a strong, conserved geometric structure in population activity (toroids and ring attractors, respectively) that is persistent across individuals and even during sleep. In all of these studies, the neural manifold view was critical in bringing that common organization to light. The activity of individual cells showed only echoes of what proved to be robust structure spanning conditions and individuals.

Ultimately, we all as scientists have diverging goals for studying the brain and different criteria for what constitutes “understanding.” (Indeed, someone could write a whole follow-up article on this nuanced topic.) However, these early examples demonstrate the capacity for neural manifolds to stoke inspiration and invite new theories into the scientific discourse. As we continue to better articulate the neural manifold framework with increasingly powerful experiments and datasets, I have no doubt that our progress will only accelerate.