The missing half of the neurodynamical systems theory

Around the turn of this century, systems neuroscience began to shift its focus from single cells to neural populations. Gilles Laurent was among the first to simultaneously record from multiple single cells in a sensory neural circuit, data that required new analytical methods. In collaboration with a mathematician, he tied the circuit’s computation—the information processing of a stimulus—to the trajectories of neural population activity in a state space. At the same time, theorists began to think about the dynamics of neural activity in multidimensional terms. They proposed attractor network models—a neural circuit in which activity patterns settle into dynamical stable states—for sensory information processing, memory and decision-making.

This pivot was the start of the dynamical systems approach to understanding how groups of neurons encode information, perform computations and accomplish tasks. Dynamical systems theory aims to predict the future evolution of a system, such as a neural circuit, based on its current state and interactions among constituent units, such as neurons. It is thus a mathematical language suited for understanding the link between neural population activity and behavior. (For more on this approach, see my recently published textbook Theoretical Neuroscience: Understanding Cognition, which highlights the modern perspective of neural circuits as dynamical systems.)

In the ensuing two decades, simultaneous recording from neurons has become commonplace, and neuroscientists—including the late Krishna Shenoy and his team—spurred a sea change in the field of neural dynamics. These days, calcium imaging and Neuropixels enable neuroscientists to monitor thousands of single neurons of animals performing cognitive tasks. As a result, the theory of dynamical systems has finally come to the fore. Methods for analyzing population trajectories in the state space, including dimensionality reduction and manifold discovery, have become predominant in the analysis of big data of neural activity.

But so far, the field has paid insufficient attention to “the other half” of the dynamical systems theory—the mathematics of bifurcations. Conjuring up the image of a fork in a road leading to two possible paths, the term denotes the phenomenon that a small change in the value of a parameter (characterizing a system’s property or an input) can lead to the sudden emergence of an entirely new behavior. Bifurcation in the theory of dynamical systems is akin to “phase transition” in statistical physics; as temperature rises above zero degrees Celsius, ice melts into water. As the kinetic energy of a fluid gradually increases, water can exhibit distinct behaviors from steady state to turbulence, characterized by complex spatiotemporal patterns with eddies on multiple scales; transitions between these states are described as bifurcations.

Here, I advocate for a full embrace of bifurcations in neuroscience as a mathematical mechanism to create novel neurodynamical behavior and functionality. Bifurcations can help explain, for example, how similarly structured circuits can give rise to diverse functions, such as association areas capable of subjective decisions, in contrast to early sensory areas dedicated to veridical stimulus coding and processing in the cerebral cortex.

T

hough the word bifurcation may sound new to some neuroscientists, the concept should be familiar. A simple example in brain research is that of a single neuron’s input-output relationship. As the amount of current injected into a neuron increases, the membrane potential becomes gradually more depolarized. When the current exceeds a threshold, the neuron undergoes an abrupt transition, repeatedly firing action potentials at a fixed periodicity, which is described as an oscillatory state. The general lesson is that a modest quantitative change of property can give rise to qualitatively novel behavior. Crucially, linear dynamical systems cannot exhibit bifurcation phenomena; only nonlinear ones do.

Why is it important to consider bifurcations in neuroscience? Let us consider the concept of the canonical local circuit, which asserts that the neocortex is made of repeats of a microcircuit motif. If so, how can we explain the differences in a primary sensory area such as V1 and “cognitive-type” regions, such as the posterior parietal cortex or prefrontal cortex? A graph theorist would point to the differences in these regions’ inputs and outputs, but that cannot be the whole story.

Though cortical regions share a generic canonical circuit organization, they also show biological heterogeneities—and bifurcations can help explain how these differences might underlie different functional capabilities. Experiments indicate that in primates, but perhaps not in rodents, excitatory-to-excitatory connections are more abundant in the prefrontal cortex (PFC) than in primary sensory areas. Computational modeling has shown that, in a generic recurrent local circuit, when the strength of recurrent excitatory connections exceeds a threshold level, stimulus-selective and self-sustained persistent activity suddenly emerges through a bifurcation (see figure). This could explain why information-specific persistent activity underlying working memory—the brain’s ability to internally maintain and manipulate information in the absence of sensory inputs—is commonly observed in the PFC.

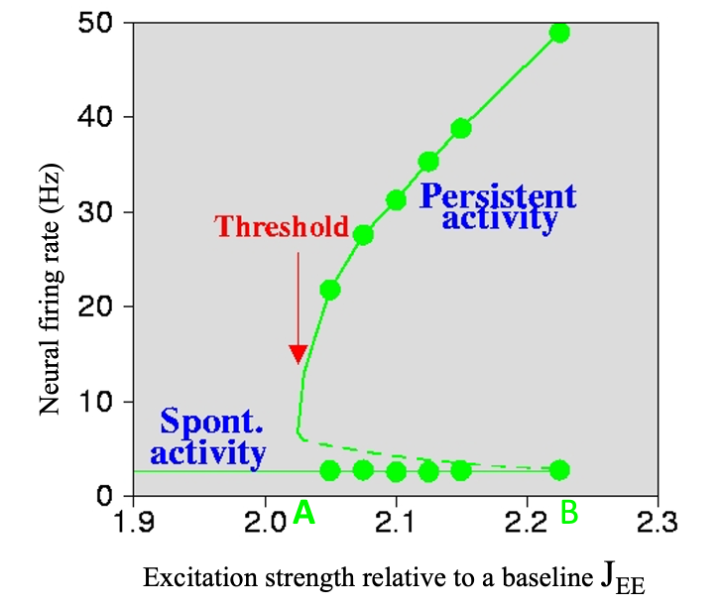
The concept of bifurcation can also illuminate why a given neural circuit can operate in different ways when some properties show modest variation. Consider the neural mechanism underlying perceptual decision-making. Work by Michael Shadlen and his colleagues revealed that when making a decision, activity in the prefrontal and posterior parietal cortices ramps up, representing the accumulation of information in favor of different choice options over time. Other studies suggested an alternative scenario in which a decision corresponds to a sudden and discrete jump from a low-firing-rate state to a high-firing-rate one, where the jumping time varies stochastically across trials. Do these two necessarily contradict each other? No, because a single neural circuit model can display either of the two regimes with modest parameter changes, thanks to a bifurcation.

As described above, the concept allows us to leverage the same canonical circuit principle for different functional capabilities in different parts of the neocortex. The primary visual cortex and prefrontal cortex may well be organized according to the same anatomical architecture, with only the latter suited to subserving working memory and decision-making merely by virtue of having more recurrent connections. I’d submit that the brain acquires increasingly sophisticated functionality through biological evolution by virtue of bifurcations in the brain; this would explain how seemingly gradual changes in brain structure can lead to the sudden emergence of an intellectual capability.

Bifurcations might also help explain a recent conundrum: The cortex is endowed with an abundance of long-range connections, with cortical areas forming a densely connected network. In such a system, it is natural to expect that neural representations are widely distributed; indeed, recent brain-wide physiological studies seemed to give the impression that one can pretty much decode any behaviorally relevant information from anywhere in the cortex, in contradiction to functional specialization in the cortex. But if that’s true, how can we explain the functional specialization of areas, such as the prefrontal cortex? My collaborators and I have proposed a theory for how bifurcation in space can support functional modularity in a multiregional cortex. Namely, despite many long-range connections, a sharp bifurcation at a specific location gives rise to a functional module that subserves working memory or subjective decision-making. This idea can, in principle, be extended to other brain functions.

The concept of bifurcation in space can therefore reconcile functional specialization and distributed neural processing over a complex brain of many parcellated regions. This idea has already been realized in a connectome-based model we built of the primate cortex, which mechanistically accounts for “ignition”—an all-or-none, widespread burst of activity thought to be a physiological marker of awareness.

Looking forward, bifurcations may provide a new way of thinking about how brain activity goes awry in disease; they offer a way to examine how modest biological changes can sometimes lead to the dramatic symptoms and behaviors associated with brain diseases. This possibility remains to be explored in future research in computational psychiatry.