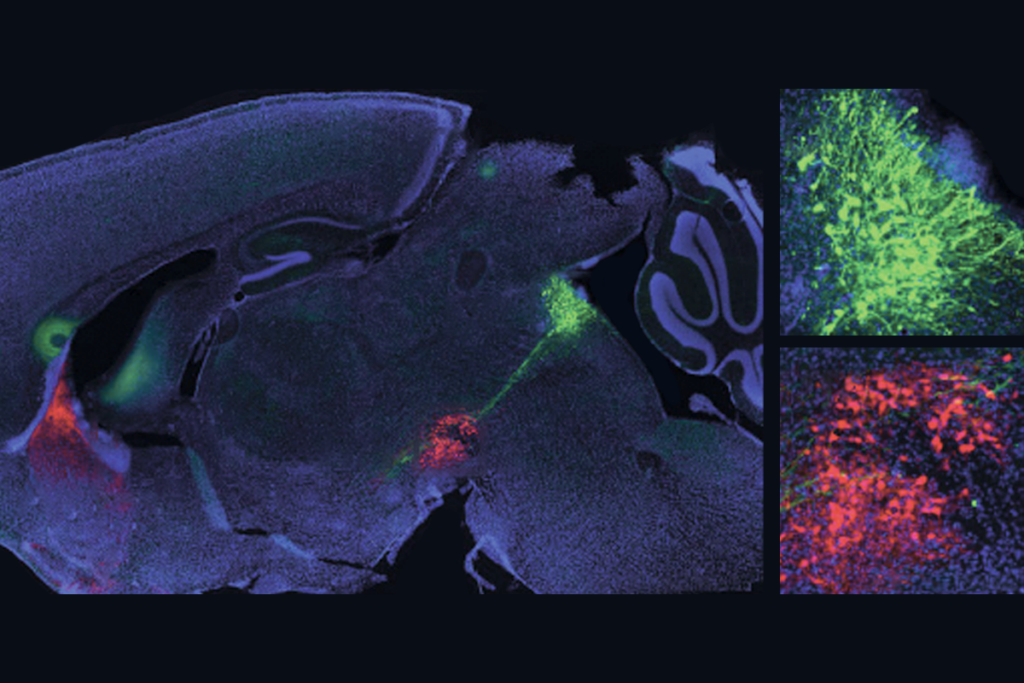
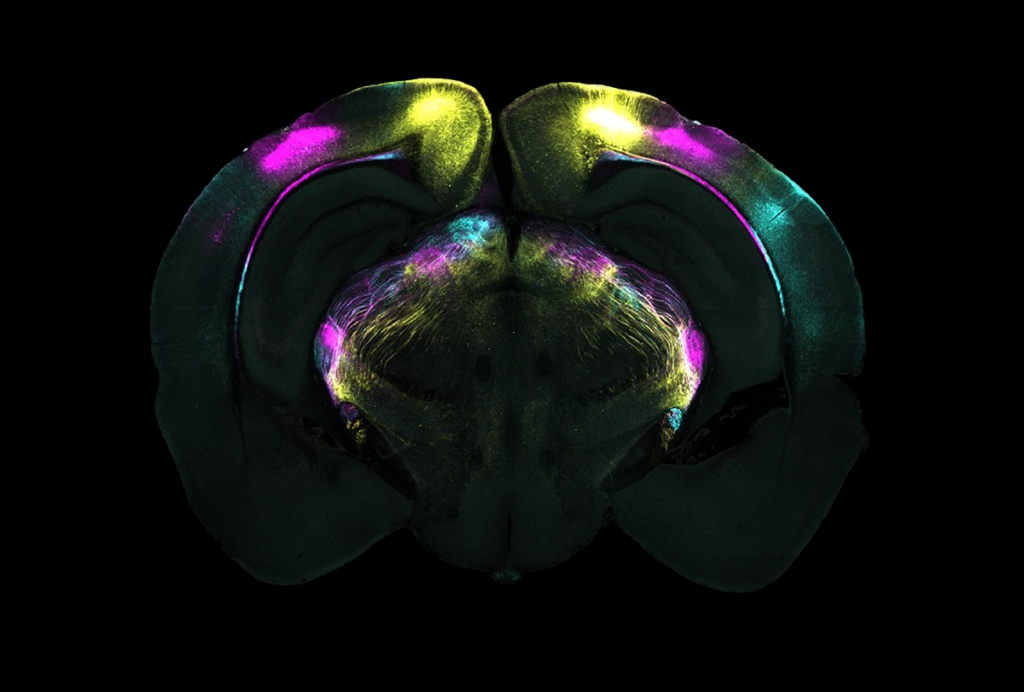
Bootstrapping
Animals with simple distributed nerve nets, like Hydra, show little evidence of learning in any form that a behavioral experimentalist would recognize, though every cell does continually regulate its own biophysics to ensure that it remains responsive to whatever signals it receives—a form of local learning. This is consistent with the idea that these earliest nerve nets serve only secondarily for sensing the environment, having first evolved to help muscles coordinate coherent movement.
Rudimentary behavioral learning arises the moment anything like a brain appears, because, at this point, neurons in the head must begin jointly adapting to changing conditions in the outside world. Every connection or potential connection between one neuron and another offers a parameter—a degree of coupling—that can be modulated to suit the circumstances, even if the “wiring diagram” is genetically preprogrammed or random. To see why, let’s take the neuron’s point of view, and imagine that it is simply trying to do the same thing any living thing does: predict and bring about its own continued existence. Some aspects of this prediction will certainly have been built in by evolution. For example, if dopamine is a proxy for food nearby, the neuron will try to predict (and thereby bring about) the presence of dopamine, because prolonged absence of dopamine implies that the whole animal will starve—bringing an end to this one neuron, along with all of its cellular clones.
Even a humble cell has plenty of needs and wants beyond food, but without food, there is no future.
Therefore, if the neuron is not itself dopamine-emitting, but its activity somehow influences dopamine in the future, it will try to activate at times that increase future dopamine. Aside from neuromodulators like dopamine, the neuron’s inputs come either from other neurons or, if it’s a sensory neuron, from an external source, such as light or taste. It can activate spontaneously, or in response to any combination of these inputs, depending on its internal parameters and degree of coupling with neighboring neurons. Presumably, at least one of its goals thus becomes fiddling with its parameters such that, when the neuron fires, future dopamine is maximized. I’ve just described a basic reinforcement learning algorithm, where dopamine is the reward signal. As brains became more complicated, though, they began to build more sophisticated models of future reward, and, accordingly, in vertebrates, dopamine appears to have been repurposed to power something approximating a more sophisticated reinforcement learning algorithm: “temporal difference” or “TD” learning. TD learning works by continually predicting expected reward and updating this predictive model based on actual reward. The method was invented (or, arguably, discovered) by Richard Sutton while he was still a grad student working toward his Ph.D. in psychology at UMass Amherst in the 1980s. Sutton aimed to turn existing mathematical models of Pavlovian conditioning into a machine learning algorithm. The problem was, as he put it, that of “learning to predict, that is, of using past experience with an incompletely known system to predict its future behavior.” In standard reinforcement learning, such predictions are goal-directed. The point is to reap a reward—like getting food or winning a board game. However, the “credit assignment problem” makes this difficult: A long chain of actions and observations might lead to the ultimate reward, but creating a direct association between action and reward can only enable an agent to learn the last step in this chain.
As Sutton put it, “whereas conventional prediction-learning methods assign credit by means of the difference between predicted and actual outcomes, [TD learning] methods assign credit by means of the difference between temporally successive predictions.” By using the change in estimated future reward as a learning signal, it becomes possible to say whether a given action is good (hence should be reinforced) or bad (hence should be penalized) before the game is lost or won, or the food is eaten.
This may sound circular, because if we already had an accurate model of the expected reward for every action, we wouldn’t need to learn anything further; why not just take the action with the highest expected reward? As in many statistical algorithms, though, by separating the problem into alternating steps based on distinct models, it’s possible for these models to take turns improving each other, an approach known as “bootstrapping”—after that old saying about the impossibility of lifting oneself up by one’s own bootstraps. Here, though, it is possible. In the TD learning context the two models are often described as the “actor” and the “critic”; in modern implementations, the actor’s model is called a “policy function” and the critic’s model, for estimating expected reward, is the “value function.” These functions are usually implemented using neural nets. The critic learns by comparing its predictions with actual rewards, which are obtained by performing the moves dictated by the actor, while the actor improves by learning how to perform moves that maximize expected reward according to the critic.
A TD learning system eventually figures out how to perform well, even if both the actor and critic are initially entirely naive, making random decisions—provided that the problem isn’t too hard, and that random moves occasionally produce a reward. Hence an experiment in the 1990s applying TD learning to backgammon worked beautifully, although applying the same method to complex games failed, at least initially.